How to solve Fourier Series problem R?
Fourier series is a mathematical tool used to represent periodic functions as a sum of sine and cosine functions (harmonics). This representation is valuable in various fields, including physics, engineering, signal processing, and mathematics. The primary idea behind the Fourier series is that any periodic function can be decomposed into a combination of simpler sinusoidal functions.
Here's a breakdown of the key concepts and components of the Fourier series:
Periodic Function: The Fourier series is primarily applicable to periodic functions, meaning they repeat themselves over a specific interval. The period of the function is denoted as "T."
Harmonics: A harmonic is a sinusoidal function with a frequency that is an integer multiple of the fundamental frequency. The fundamental frequency corresponds to the reciprocal of the period, i.e., f0 = 1/T. The harmonics are often denoted as f0, 2f0, 3f0, and so on.
Coefficient Calculation: The Fourier series representation of a periodic function, denoted as "f(x)," involves calculating the coefficients (a0, a1, a2, ..., an) and (b1, b2, ..., bn) for the sine and cosine terms, respectively. These coefficients quantify how much of each harmonic is needed to approximate the original function. They are calculated using specific formulas that depend on the function itself.
The coefficient a0 represents the average value of the function over one period and is related to the DC component.
The coefficients an and bn represent the amplitudes of the cosine and sine components of the harmonics.
Fourier Series Representation: The Fourier series representation of the periodic function f(x) is typically written as:
r
Copy code
f(x) = a0/2 + Σ [an * cos(2πn/T * x) + bn * sin(2πn/T * x)]
Here, the summation goes over all the harmonics (n = 1, 2, 3, ...) up to some finite or infinite value, depending on the desired level of accuracy.
Convergence: The quality of the Fourier series approximation depends on the number of harmonics included in the sum. Adding more harmonics generally provides a closer approximation to the original function. In practice, convergence may be finite (i.e., a finite number of terms yields a satisfactory approximation) or achieved in the limit as the number of terms approaches infinity.
Applications: Fourier series are widely used in various applications, including analyzing and synthesizing periodic signals, solving partial differential equations, image processing, and audio signal processing, such as in the compression of audio files (e.g., MP3).
Discrete Fourier Series: In some applications, it's necessary to work with discrete data, such as digital signals. The Discrete Fourier Series (DFS) is a variation of the Fourier series tailored for discrete data, often implemented using the Fast Fourier Transform (FFT) algorithm for efficient computation.
Overall, the Fourier series provides a powerful mathematical framework for analyzing and representing periodic functions by breaking them down into their constituent sinusoidal components, making them a fundamental tool in many areas of science and engineering.
> library("dplyr", lib.loc="~/R/win-library/3.6")
> library("ggplot2", lib.loc="~/R/win-library/3.6")
install.packages("purrrlyr", dependencies = FALSE)
install.packages("purrr", dependencies = FALSE)
library("dplyr", lib.loc="~/R/win-library/3.6")
> library("lattice", lib.loc="C:/Program Files/R/R-3.6.1/library")
> df <- 5
> cf <- function(t) (1 - 2i*t)^(-df/2)
> dens <- function(x) dchisq(x, df)
> ## Set resolutions
> resolutions <- 2^(6:8)
> ## Compute integral given the resolution
> recover_f <- function(resol){
+ ## Get grid and density values
+ out <- fourierin(f = cf, lower_int = -10, upper_int = 10,
+ lower_eval = -3, upper_eval = 20,
+ const_adj = -1, freq_adj = -1,
+ resolution = resol)
+ ## Return in data frame format
+ out %>%
+ as_data_frame() %>%
+ transmute(
+ x = w,
+ values = Re(values),
+ resolution = resol)
+ }
> vals <- map_df(resolutions, recover_f)
>
> true <- data_frame(x = seq(min(vals$x), max(vals$x), length = 150),
+ values = dens(x))
Warning message:
`data_frame()` is deprecated, use `tibble()`.
This warning is displayed once per session.
>
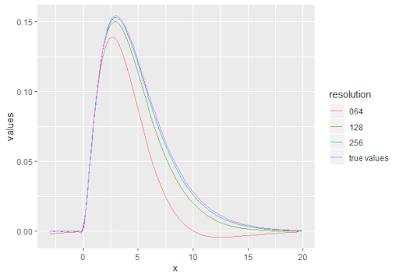
> univ_plot <-
+ vals %>%
+ mutate(resolution = as.character(resolution),
+ resolution = gsub("64", "064", resolution)) %>%
+ ggplot(aes(x, values)) +
+ geom_line(aes(color = resolution)) +
+ geom_line(data = true, aes(color = "true values"))
> univ_plot
> set.seed(666)
> new_grid <- rchisq(n = 3, df = df)
> resolutions <- 2^(6:9)
> fourierin(f = cf, lower_int = -10, upper_int = 10,
+ eval_grid = new_grid,
+ const_adj = -1, freq_adj = -1,
+ resolution = 128) %>%
+ c () %>% Re() %>%
+ data_frame(x = new_grid, fx = .)
# A tibble: 3 x 2
x fx
<dbl> <dbl>
1 6.41 0.0874
2 11.7 0.0152
3 3.06 0.154
> approximated_fx <- function (resol) {
+ fourierin(f = cf, lower_int = -10, upper_int = 12,
+ eval_grid = new_grid,
+ const_adj = -1, freq_adj = -1,
+ resolution = resol) %>%
+ c() %>% Re() %>%
+ {data_frame(x = new_grid,
+ fx = dens(new_grid),
+ diffs = abs(. - fx),
+ resolution = resol)}
+ }
>
> tab <-
+ map_df(resolutions, approximated_fx) %>%
+ arrange(x) %>%
+ mutate(diffs = round(diffs, 7)) %>%
+ rename('f(x)' = fx,
+ 'absolute difference' = diffs)
> tab
# A tibble: 12 x 4
x `f(x)` `absolute differe~ resolution
<dbl> <dbl> <dbl> <dbl>
1 3.06 0.154 0.000207 64
2 3.06 0.154 0.0000476 128
3 3.06 0.154 0.0000472 256
4 3.06 0.154 0.0000471 512
5 6.41 0.0874 0.000078 64
6 6.41 0.0874 0.0000155 128
7 6.41 0.0874 0.0000148 256
8 6.41 0.0874 0.0000147 512
9 11.7 0.0152 0.0000097 64
10 11.7 0.0152 0.0000025 128
11 11.7 0.0152 0.0000022 256
12 11.7 0.0152 0.0000022 512
> library("dplyr", lib.loc="~/R/win-library/3.6")
> library("lattice", lib.loc="C:/Program Files/R/R-3.6.1/library")
mu <- c(-1, 1)
> sig <- matrix(c(3, -1, -1, 2), 2, 2)
> f <- function(x) {
+ ## Auxiliar values
+ d <- ncol(x)
+ z <- sweep(x, 2, mu, "-")
+ ## Get numerator and denominator of normal density
+ num <- exp(-0.5*rowSums(z * (z %*% solve(sig))))
+ denom <- sqrt((2*pi)^d*det(sig))
+ return(num/denom)
+ }
>
> ## Characteristic function, s is n x d
> phi <- function (s) {
+ complex(modulus = exp(-0.5*rowSums(s*(s %*% sig))),
+ argument = s %*% mu)
+ }
> ## Evaluate characteristic function for a given resolution.
> eval <- fourierin(f,
+ lower_int = c(-8, -6), upper_int = c(6, 8),
+ lower_eval = c(-4, -4), upper_eval = c(4, 4),
+ const_adj = 1, freq_adj = 1,
+ resolution = 2*c(64, 64),
+ use_fft = T)
> ## Evaluate true and approximated values of Fourier integral
> dat <- eval %>%
+ with(crossing(y = w2, x = w1) %>%
+ mutate(approximated = c(values))) %>%
+ mutate(true = phi(matrix(c(x, y), ncol = 2)),
+ difference = approximated - true) %>%
+ gather(value, z, -x, -y) %>%
+ mutate(real = Re(z), imaginary = Im(z)) %>%
+ select(-z) %>%
+ gather(part, z, -x, -y, -value)
Error in crossing(y = w2, x = w1) : could not find function "crossing"
> wireframe(z ~ x*y | value*part, data = dat,
+ scales =
+ list(arrows=FALSE, cex= 0.45,
+ col = "black", font = 3, tck = 1),
+ screen = list(z = 90, x = -74),
+ colorkey = FALSE,
+ shade=TRUE,
+ light.source= c(0,10,10),
+ shade.colors = function(irr, ref,
+ height, w = 0.4)
+ grey(w*irr + (1 - w)*(1 - (1 - ref)^0.4)),
+ aspect = c(1, 0.65))
Error in wireframe.formula(z ~ x * y | value * part, data = dat, scales = list(arrows = FALSE, :
object 'dat' not found
>
> mu <- c(-1, 1)
> sig <- matrix(c(3, -1, -1, 2), 2, 2)
> f <- function(x) {
+ ##-Auxiliary values
+ d <- ncol(x)
+ z <- sweep(x, 2, mu, "-")
+ ##-Get the numerator and denominator of normal density
+ num <- exp(-0.5*rowSums(z * (z %*% solve(sig))))
+ denom <- sqrt((2*pi)^d*det(sig))
+
+ return(num/denom)
+ }
> phi <- function(s) {
+ complex(modulus = exp(- 0.5*rowSums(s*(s %*% sig))),
+ argument = s %*% mu)
+ }
>
> eval <- fourierin_2d(f, lower_int = c(-8, -6), upper_int = c(6, 8),
+ lower_eval = c(-4, -4), upper_eval = c(4, 4),
+ const_adj = 1, freq_adj = 1,
+ resolution = c(128, 128))
>
> t1 <- eval$w1
> t2 <- eval$w2
> t <- as.matrix(expand.grid(t1 = t1, t2 = t2))
> approx <- eval$values
> true <- matrix(phi(t), 128, 128) # Compute true values
>
> i <- 65
> plot(t2, Re(approx[i, ]), type = "l", col = 2,
+ ylab = "",
+ xlab = expression(t[2]),
+ main = expression(paste("Real part section at ",
+ t[1], "= 0")))
> lines(t2, Re(true[i, ]), col = 3)
> legend("topleft", legend = c("true", "approximation"),
+ col = 3:2, lwd = 1)
> plot(t1, Im(approx[, i]), type = "l", col = 2,
+ ylab = "",
+ xlab = expression(t[1]),
+ main = expression(paste("Imaginary part section at ",
+ t[2], "= 0")))
> lines(t1, Im(true[, i]), col = 3)
> legend("topleft", legend = c("true", "approximation"),
+ col = 3:2, lwd = 1)
> > myfnc <- function(t) exp(-t^2/2)
> out <- fourierin(f = myfnc, lower_int = -5, upper_int = 5,
+ lower_eval= -3, upper_eval = 3, const_adj = -1,
+ freq_adj = -1, resolution = 64)
> grid <- out$w
> values <- Re(out$values)
> plot(grid, values, type = "l", col = 3)
> lines(grid, dnorm(grid), col = 4)
> myfnc <- function(t) dgamma(t, shape, rate)
> shape <- 5
> rate <- 3
> out <- fourierin(f = myfnc, lower_int = 0, upper_int = 6,
+ lower_eval = -4, upper_eval = 4,
+ const_adj = 1, freq_adj = 1, resolution = 64)
>
> grid <- out$w
> re_values <- Re(out$values)
> im_values <- Im(out$values)
> true_cf <- function(t, shape, rate) (1 - 1i*t/rate)^-shape
> true_re <- Re(true_cf(grid, shape, rate))
> true_im <- Im(true_cf(grid, shape, rate))
> plot(grid, re_values, type = "l", col = 3)
> lines(grid, true_re, col = 4)
> plot(grid, im_values, type = "l", col = 3)
> lines(grid, true_im, col = 4)
> mu <- c(-1, 1)
> sig <- matrix(c(3, -1, -1, 2), 2, 2)
> f <- function(x) {
+ ##-Auxiliary values
+ d <- ncol(x)
+ z <- sweep(x, 2, mu, "-")
+ ##-Get the numerator and denominator of normal density
+ num <- exp(-0.5*rowSums(z * (z %*% solve(sig))))
+ denom <- sqrt((2*pi)^d*det(sig))
+ return(num/denom)
+ }
>
> phi <- function(s) {
+ complex(modulus = exp(- 0.5*rowSums(s*(s %*% sig))),
+ argument = s %*% mu)
+ }
> eval <- fourierin(f, lower_int = c(-8, -6), upper_int = c(6, 8),lower_eval = c(-4, -4), upper_eval = c(4, 4),const_adj = 1, freq_adj = 1,resolution = c(128, 128))
>
> t1 <- eval$w1
> t2 <- eval$w2
> t <- as.matrix(expand.grid(t1 = t1, t2 = t2))
> approx <- eval$values
> true <- matrix(phi(t), 128, 128)
> i <- 65
> plot(t2, Re(approx[i, ]), type = "l", col = 2,
+ ylab = "",
+ xlab = expression(t[2]),
+ main = expression(paste("Real part section at ",t[1], "= 0")))
> lines(t2, Re(true[i, ]), col = 3)
> legend("topleft", legend = c("true", "approximation"),
+ col = 3:2, lwd = 1)
> plot(t1, Im(approx[, i]), type = "l", col = 2,
+ ylab = "",
+ xlab = expression(t[1]),
+ main = expression(paste("Imaginary part section at ",t[2], "= 0")))
> lines(t1, Im(true[, i]), col = 3)
> legend("topleft", legend = c("true", "approximation"),
+ col = 3:2, lwd = 1)
Learn PYTHON



0 Comments