CORRELATION DEFINITIONS

Correlation  in Statistics

CORRELATION DEFINITIONS

Correlation means two quantitative facts having the relationship of cause and effect varying simultaneously in the same or in the opposite directions, the measurement of such variations.

Correlation definition according to L.R.Conner "If two or more quantities vary in sympathy so that movements in the one tend to be accompanied by corresponding movements in the other, then they are said to be correlated".

Correlation definition according to King "Correlation means that between two series or groups of data, there exists some casual connections".

Correlation definition according to Croxton and Cowden "When the relationship is of a quantitative nature, the appropriate statistical tool for discovering and measuring the relationship and expressing it in a brief formula is known as correlation".

Correlation definition according to W.A.Neiswanger "Correlation analysis contributes to the understanding of economic behavior, aids in locating critically important variables on which others depend may reveal to the economist the connections by which disturbances spread and suggest to him the paths through which stabilizing forces many become effective".

Correlation is a statistical concept that measures the degree to which two variables are related or associated with each other. It quantifies the strength and direction of the relationship between two or more variables, helping to understand how changes in one variable may be associated with changes in another.

Key points about correlation include:

Strength of Relationship: Correlation indicates how strong the relationship between variables is. It can range from -1 to 1, with -1 indicating a perfect negative correlation (as one variable increases, the other decreases), 1 indicating a perfect positive correlation (both variables increase together), and 0 indicating no correlation (no apparent relationship).

Direction of Relationship: Correlation also provides information about the direction of the relationship. Positive correlation means that as one variable increases, the other tends to increase as well, while negative correlation implies that as one variable increases, the other tends to decrease.

Scatterplots: Correlation is often visualized using scatterplots, where each data point represents a combination of values for the two variables. A positive correlation appears as a trend where data points cluster in an upward direction, while a negative correlation shows a downward trend.

Pearson Correlation Coefficient: The most common method to calculate correlation is the Pearson correlation coefficient (r). It measures linear relationships between variables. It is calculated by dividing the covariance of the two variables by the product of their standard deviations. The formula for the Pearson correlation coefficient is:

Pearson Correlation Coefficient Formula

are the means of the respective variables.

Sensitivity to Outliers: Correlation is sensitive to outliers, which can significantly influence the calculated correlation coefficient. Extreme values in the data can either inflate or deflate the apparent strength of the relationship.

Causation: It's important to note that correlation does not imply causation. Just because two variables are correlated does not mean that one causes the other. There may be underlying factors or third variables affecting both variables simultaneously.

In summary, correlation is a statistical measure used to quantify the relationship between two or more variables, helping researchers and analysts understand the strength and direction of this relationship. It is a valuable tool in various fields, including statistics, economics, social sciences, and many others, for exploring patterns and making predictions.

Perfect Correlation

When the movement in two related variables is in the same direction and in the same proportion, it is a perfect positive correlation. The coefficient of correlation(r) in this case will be +1. On the other hand, if changes are proportional but in the opposite direction, it will be a perfect negative correlation and its calculated value will be -1.

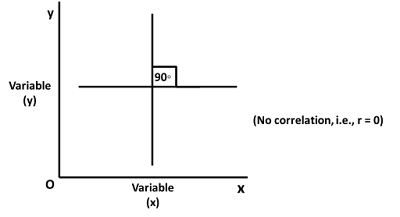
Absence of Correlation

If no independence is found between two variables or there is no relationship between deviation in one variable to corresponding deviations in the other variable, it is the situation of absence of correlation and in this case coefficient of correlation will be zero.

                

The correlation coefficient is a single-number summary expressing the utility of linear regression. a correlation coefficient is a dimensionless number between - 1 and + 1. The slope and the correlation have the same positive or negative sign. This single number is used to convey the strength of a linear relationship, so values closer to - 1 or + 1 indicate greater fidelity to a straight-line relationship. 

The correlation is standardized in the sense that its value does not depend on the means or standard deviations of the x or y values.

If we add or subtract the same values from the data (and thereby change the means ), the correlation remains the same. If we multiply all the xs (or the ys)by some positive value, the correlation remains the same. If we multiply either the xs or the ys by a negative number, the sign of the correlation will reverse.                                  

As with any oversimplification of a complex situation, the correlation coefficient has its benefits, but also its shortcomings. A variety of values of the correlation are illustrated. Each of these separate graphs consists of 50 simulated pairs of observations. A correlation of 0 in the upper left of no indication of a linear relationship between the plotted variables. A correlation of 0.4 does not indicate much strength, and A correlation of either 0.8 or 0.9 indicates a rather strong linear trend.

Importance of correlation

More Reliable Forecasting: It is important, to mention that business forecasting is an important aspect of the decision-making process in the business world.

Correlation is useful in research, the technique of correlation proves very useful in making analyses, drawing conclusions, and developing hypotheses and theories in the area of research and investigation.

Study of Economic Activity: Correlation is also useful in the analytical study of economic activities. For example, it is very useful in studying the impact of price change on the change in demand, of change in the supply of money on the price of money, and variation in the production of cotton on the production of cloth, etc.

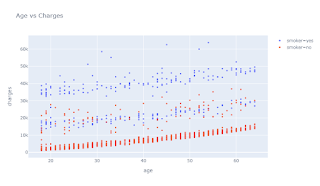
Correlation analysis in Python

 Data has been taken from GitHub

from urllib.request import urlretrieve

urlretrieve(medical_charges_url,'medical-charges.csv')

('medical-charges.csv', <http.client.HTTPMessage at 0x7f159ec4ec50>)

import pandas as pd

medical_df = pd.read_csv('medical-charges.csv')

medical_df

age	sex	bmi	children	smoker	region	charges
0	19	female	27.900	0	yes	southwest	16884.92400
1	18	male	33.770	1	no	southeast	1725.55230
2	28	male	33.000	3	no	southeast	4449.46200
3	33	male	22.705	0	no	northwest	21984.47061
4	32	male	28.880	0	no	northwest	3866.85520
...	...	...	...	...	...	...	...
1333	50	male	30.970	3	no	northwest	10600.54830
1334	18	female	31.920	0	no	northeast	2205.98080
1335	18	female	36.850	0	no	southeast	1629.83350
1336	21	female	25.800	0	no	southwest	2007.94500
1337	61	female	29.070	0	yes	northwest	29141.36030

1338 rows × 7 columns

medical_df.info()

<class 'pandas.core.frame.DataFrame'> RangeIndex: 1338 entries, 0 to 1337 Data columns (total 7 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 age 1338 non-null int64 1 sex 1338 non-null object 2 bmi 1338 non-null float64 3 children 1338 non-null int64 4 smoker 1338 non-null object 5 region 1338 non-null object 6 charges 1338 non-null float64 dtypes: float64(2), int64(2), object(3) memory usage: 73.3+ KB

medical_df.describe()

	age	bmi	children	charges
count	1338.000000	1338.000000	1338.000000	1338.000000
mean	39.207025	30.663397	1.094918	13270.422265
std	14.049960	6.098187	1.205493	12110.011237
min	18.000000	15.960000	0.000000	1121.873900
25%	27.000000	26.296250	0.000000	4740.287150
50%	39.000000	30.400000	1.000000	9382.033000
75%	51.000000	34.693750	2.000000	16639.912515
max	64.000000	53.130000	5.000000	63770.428010

# Exploratory Analysis and  Visualisation

import plotly. express as pt

import matplotlib

import matplotlib.pyplot as plt

import seaborn as sns

%matplotlib inline

sns.set_style('darkgrid')

matplotlib.rcParams['font.size']=14

matplotlib.rcParams['figure.figsize']=(20,4)

matplotlib.rcParams['figure.facecolor']='#00000000'

medical_df.age.describe()

count 1338.000000 mean 39.207025 std 14.049960 min 18.000000 25% 27.000000 50% 39.000000 75% 51.000000 max 64.000000 Name: age, dtype: float64

fig=pt.histogram(medical_df,

                 x='age',

                 marginal='box',

                 nbins=47,

    title='Distribition of Age')

fig.update_layout(bargap=0.1)

fig.show()

fig= pt.histogram(medical_df,

                  x='bmi',

                  marginal='box',

                  color_discrete_sequence=['red'],

                  title='Distribution of BMI(Body Mass Index)' )

fig.update_layout(bargap=0.1)

fig.show()

fig = pt.histogram(medical_df,

                 x='charges',

                 marginal='box',

                 color='smoker',

                 color_discrete_sequence=['green','grey'],

                 title='Annual Medical Charges' )

fig.update_layout(bargap=0.1)

fig.show( )

fig = pt.histogram(medical_df,

                 x='sex',

                 marginal='box',

                 color='region',

                 color_discrete_sequence=['green','grey'],

                 title='Annual Medical Charges' )

fig.update_layout(bargap=0.1)

fig.show( )

medical_df.smoker.value_counts()

no 1064 yes 274 Name: smoker, dtype: int64

pt.histogram(medical_df,x='smoker',color='sex',title='smoker')

#Visualize the relationship between 'age ' 

and 'charges

fig =pt.scatter(medical_df,

                x='age',

                y='charges',

                color='smoker',

                opacity=0.8,

                hover_data=['sex'],

                title='Age vs Charges')

fig.update_traces(marker_size=5)

fig.show()

fig =pt.scatter(medical_df,

                x='bmi',

                y='charges',

                color='smoker',

                opacity=0.8,

                hover_data=['sex'],

                title='BMI vs Charges')

fig.update_traces(marker_size=5)

fig.show()

pt.scatter(medical_df,x='children',y='charges')

pt.violin(medical_df,x='children',y='charges')

Machine learning book

#Correlation

medical_df.charges.corr(medical_df.age)

0.2990081933306476

medical_df.charges.corr(medical_df.bmi)

0.19834096883362895

smoker_values={'no': 0,'yes': 1}

smoker_numeric =medical_df.smoker.map(smoker_values)

medical_df.charges.corr(smoker_numeric)

0.787251430498478

pt.scatter(medical_df,x='age',y='age')

Statistics book in Python

pt.scatter(medical_df,x='age',y='children')

medical_df.corr()

	age	bmi	children	charges
age	1.000000	0.109272	0.042469	0.299008
bmi	0.109272	1.000000	0.012759	0.198341
children	0.042469	0.012759	1.000000	0.067998
charges	0.299008	0.198341	0.067998	1.000000

sns.heatmap(medical_df.corr(),cmap='Reds',annot=True)

plt.title('Correlation Matrix');

More related updates on correlation in Python

RegrassionAnalysis Used for

PYTHON